¡Bienvenidos al blog del CBTa 224 - 01 Extensión Petaquillas! Nos complace darles la bienvenida al Centro de Bachillerato Tecnológico Agropecuario CBTa 224 - 01 Extensión Petaquillas. Aquí, nos comprometemos a ofrecer una educación de calidad en el nivel medio superior, proporcionando a nuestros estudiantes no solo una sólida formación académica, sino también la oportunidad de especializarse en carreras técnicas que los prepararán para el mundo laboral. En nuestro centro, ofrecemos dos especialidades técnicas: Técnico Agropecuario y Técnico en Ofimática. Estas opciones permiten a nuestros alumnos adquirir habilidades prácticas y conocimientos avanzados que los posicionan para destacar en el ámbito agrícola y en el entorno administrativo y tecnológico. Nuestro enfoque educativo está diseñado para fomentar el desarrollo integral de los estudiantes, combinando teoría y práctica en un entorno de aprendizaje dinámico y colaborativo. Creemos firmemente en la importancia de preparar a l...
Módulo de Young o Módulo de Elasticidad Longitudinal: Conceptos, Aplicaciones y Comparaciones
El Módulo de Young, también conocido como módulo de
elasticidad longitudinal, es uno de los conceptos fundamentales en el estudio
de la resistencia de materiales, particularmente en ingeniería y construcción.
Este módulo mide la capacidad de un material para resistir la deformación
cuando se le aplica una tensión. En este artículo, profundizaremos en su
definición, fórmula, su relación con la tensión y la deformación unitaria, así
como su importancia en la práctica.
Definición del Módulo
de Young
\[
E = \frac{\sigma}{\varepsilon}
\]
Donde:
- \(E\) es el Módulo de Young (en pascales, Pa),
- \(\sigma\) es la tensión (fuerza por unidad de área, en pascales, Pa),
- \(\varepsilon\) es la deformación unitaria (cambio en la longitud original sin unidades).
En términos sencillos, el módulo de Young cuantifica la rigidez
de un material: un valor alto indica un material más rígido, mientras que un
valor bajo sugiere que el material es más flexible.
Relación entre Tensión y Deformación Unitaria
La relación entre la tensión (\(\sigma\)) y la deformación unitaria (\(\varepsilon\)) es lineal dentro del rango elástico del material, es decir, mientras no se exceda el límite elástico, esta relación se mantiene. La tensión se define como la fuerza aplicada por unidad de área (\(F/A\)):
\[ \sigma = \frac{F}{A} \]
La deformación unitaria se calcula como el cambio de longitud del material respecto a su longitud original:
\[
\varepsilon = \frac{\Delta L}{L_0}
\]
Donde:
- \( \Delta L \) es el cambio en la longitud,
- \( L_0 \) es la longitud original del material.
Por lo tanto, mientras más grande sea el módulo de Young de un material, mayor será la fuerza que este puede soportar antes de deformarse permanentemente.
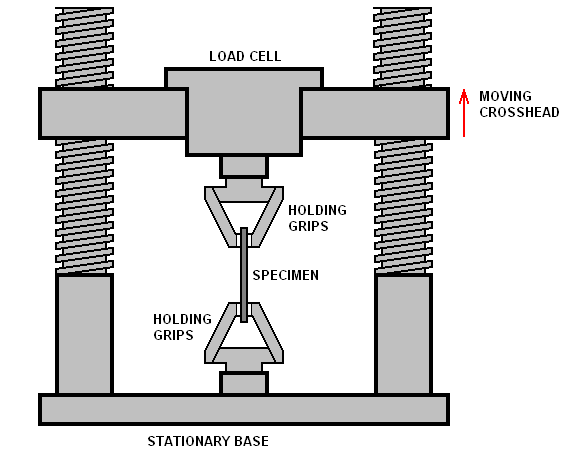
Gráficas de Tensión-Deformación para Diferentes Materiales
En el análisis de materiales, es común utilizar gráficas de tensión-deformación para describir el comportamiento mecánico bajo carga. Estas gráficas muestran cómo un material responde a una fuerza aplicada. Aquí se observan tres fases principales:
1. Región elástica: Donde el material puede recuperar su forma original después de la descarga. La pendiente de la curva en esta región es el módulo de Young.
2. Región plástica: Si se excede el límite elástico, el material comienza a deformarse permanentemente.
3. Fractura: Finalmente, si la tensión continúa aumentando, el material alcanzará su límite de ruptura.
A continuación, un resumen de cómo varían estas gráficas según el tipo de material:
- Materiales dúctiles: Como el acero, presentan una clara región elástica seguida de una región plástica antes de la fractura. Pueden deformarse considerablemente antes de romperse.
- Materiales frágiles: Como el vidrio, tienen una curva casi lineal hasta la fractura, con poca o ninguna deformación plástica, rompiéndose abruptamente después de superar su límite elástico.
Comparación del Módulo de Elasticidad en Materiales Dúctiles y Frágiles
El módulo de elasticidad varía significativamente entre los materiales dúctiles y frágiles:
- Materiales Dúctiles: Son aquellos que pueden soportar grandes deformaciones antes de fracturarse. Un ejemplo típico es el acero. Estos materiales tienen un módulo de Young elevado, lo que indica que pueden resistir altas tensiones mientras se deforman de manera considerable.
Ejemplo: El módulo de Young del acero es de aproximadamente \(200 \times 10^9 \, \text{Pa}\) (200 GPa).
- Materiales Frágiles: Estos materiales se rompen sin sufrir deformaciones significativas. El vidrio y la cerámica son buenos ejemplos de materiales frágiles. Aunque algunos de ellos pueden tener un módulo de Young alto, son incapaces de soportar grandes deformaciones.
Ejemplo: El vidrio tiene un módulo de Young de aproximadamente \(70 \times 10^9 \, \text{Pa}\) (70 GPa), pero se fractura rápidamente bajo tensión.
Aplicaciones en Ingeniería y Construcción
El Módulo de Young es un parámetro esencial en la ingeniería y la construcción porque proporciona información sobre cómo se comportará un material cuando se le aplique una fuerza. Algunas de sus aplicaciones más importantes incluyen:
1. Diseño estructural: En el diseño de puentes, rascacielos, carreteras, y otras infraestructuras, los ingenieros seleccionan los materiales basándose en su módulo de Young para garantizar que las estructuras puedan soportar las tensiones y las cargas sin deformarse significativamente.
2. Fabricación de herramientas y maquinaria: En la industria manufacturera, el módulo de Young se utiliza para seleccionar materiales que puedan resistir tensiones repetidas sin deformarse, como en el caso de resortes, cables de acero, y otras piezas mecánicas.
3. Componentes aeroespaciales y automotrices: En la construcción de aviones y automóviles, los materiales con un alto módulo de Young, como el aluminio y el titanio, se prefieren debido a su capacidad para soportar grandes tensiones mientras mantienen un peso bajo.
4. Aplicaciones médicas: En ortopedia y odontología, el módulo de Young de materiales como el titanio se utiliza para desarrollar implantes y prótesis que puedan soportar las cargas del cuerpo humano sin deformarse.
5. Electrónica: Los materiales con módulos de Young específicos son seleccionados para garantizar la integridad estructural en dispositivos electrónicos que están sujetos a tensiones térmicas o mecánicas durante su funcionamiento.
Conclusión
El Módulo de Young es una propiedad mecánica fundamental que describe la rigidez de un material y su capacidad para resistir la deformación bajo tensión. En aplicaciones prácticas, es crucial para el diseño y selección de materiales en proyectos de ingeniería, construcción, manufactura, y muchos otros campos. Comprender la relación entre la tensión y la deformación unitaria, así como las diferencias en el comportamiento entre materiales dúctiles y frágiles, permite a los ingenieros desarrollar soluciones seguras y eficientes. Las gráficas de tensión-deformación proporcionan una herramienta visual clave para comprender cómo se comportarán los materiales bajo cargas reales.
Comentarios
Publicar un comentario